Cómo dominar los estudiantes de puntuación verbal y adultos

Además de excelentes marcas en matemáticas, aritmética en mente da muchos beneficios a lo largo de la vida. La práctica en los cálculos sin calculadora, usted:

• Mantener su mente aguda. Para un funcionamiento eficiente del intelecto, como los músculos, necesita un entrenamiento regular. Gasto en la mente se desarrolla la memoria, el pensamiento lógico y la concentración, aumenta la capacidad de aprender, que ayuda a navegar rápidamente la situación y tomar las decisiones correctas.
• Cuidar de su salud mental. Los estudios muestranPodría cálculo mental mejorar la salud emocional?Que en cuenta la participación oral de las partes del cerebro responsables de depresión y la ansiedad. El más activo es el área de trabajo, menor es el riesgo de la neurosis y negro melancolía.
• Asegurados contra pinchazos en situaciones cotidianas. La capacidad de contar rápidamente el cambio, tamaño de la punta, el número de calorías o intereses sobre el préstamo que protege de los gastos inesperados, exceso de peso y estafas.

Aprender técnicas de conteo rápido pueden ser a cualquier edad. No importa si al principio es un poco "lento hacia abajo." La práctica diaria operaciones aritméticas básicas de 10-15 minutos, y después de un par de meses llegarán a resultados significativos.

¿Cómo aprender a poner en la mente

Resumimos un solo dígito

Comenzar a entrenar con el nivel de primaria - la adición de un solo dígito con la transición a través de docenas. Esta técnica aprender en el primer grado, pero por alguna razón, a menudo se pasa por alto con la edad.

• Supongamos que usted tiene que añadir 7 y 8.
• Contar el número de sietes no es suficiente para diez: 10 - 7 = 3.
• Spread ocho importe de tres y la segunda parte es 8 + 3 = 5.
• Agregar una segunda porción a diez 10 + 5 = 15.

La misma técnica de "confiar en los diez primeros" se utilizan en la suma de un solo dígito a de dos dígitos, de tres dígitos, y así sucesivamente. Además Hone más simple, hasta que aprenda a realizar una operación durante un par de segundos.

Resumiendo los grandes números

El principio más importante - para romper los términos de las filas (miles, centenas, decenas y unidades) y añadir el mismo el uno al otro, comenzando por el más grande.

Digamos que se agrega 1574-689.

• 1574 se descompone en cuatro clases: 1 000, 500, 70 y 4. 689 - a tres: 600, 80 y 9.
• Ahora se resumen: miles de miles (1 000 + 0 = 1 000), de cientos a cientos (500 + 600 = 1 100), decenas a decenas (70 + 80 = 150), con unidades de una unidad (4 + 9 = 13).
• Grupo el número, ya que es conveniente, y se añade el hecho de que tenemos: (1 000 + 1 100) + (150 + 13) = 2 100 + 163 = 2 263.

La principal dificultad - a tener en cuenta todos los resultados intermedios. La práctica de esta cuenta, que son al mismo tiempo tren de la memoria.

¿Cómo aprender a restar en su mente

Restar un solo dígito

Una vez más volvemos a la primera clase y perfeccionar los conocimientos restar un dígito con la transición a través de docenas.

Suponga que desea restar 8 de 35.

• Introducir 35 como la suma de 30 + 5.
• 8 no se puede restar de 5, 8 por lo descomponen la suma de 5 + 3.
• Restar 5 de 35 y 30 de obtener. Entonces, restar 30 de los tres restantes 30 - 3 = 27.

Restamos números grandes

A diferencia de la constitución, al restar números de varios dígitos en el nivel que necesita para romper sólo lo que le quitas.

Por ejemplo, se le pide que restar 347 de 932.

• El número 347 se compone de tres partes bits: 300 + 40 + 7.
• Primeros cientos restar: 932 - 300 = 632.
• Nos dirigimos a las decenas 632 - 40 años. Para mayor comodidad, el 40 se puede representar como la suma de 30 + 10. En primer lugar, restar 30 y obtener 632 - 30 = 602. Ahora resta 10 de 602 restante y obtener 592.
• Queda por hacer frente a las unidades, utilizando todos el mismo "apoyo en el top ten." En primer lugar restar de 592 deuce: 592 - 2 = 590. Entonces, lo que se deja de sietes: 7 - 2 = 5. Obtenemos 590 - 5 = 585.

¿Cómo aprender a multiplicarse en la mente

Layfhaker ya escribió sobre cómo dominar rápidamente tabla de multiplicación.

Añadimos que las mayores dificultades en los niños y adultos es la multiplicación de 7 a 8. Hay una regla simple que le ayudará a no estar equivocado en este asunto. Sólo recuerda: "cinco, seis, siete, ocho" - 56 = 7 × 8.

Y ahora vamos a pasar a los casos más complejos.

Multiplicar las cifras de un dígito en los varios valores

De hecho, todo lo que aquí es simple. La división de un número de varios valores en los bits, se multiplica cada dígito y para resumir los resultados.

Examinemos un ejemplo concreto: 759 × 8.

• Splitting mordió 759 en la porción 700, 50 y 9.
• Multiplicar cada bit individual: 700 × 8 = 5600, 50 = 400 × 8, 9 × 8 = 72.
• Doblar resultados, rompiendo en categorías: 5 600 + 400 + 72 = 5 000 + (600 + 400) + 72 = 5 000 + 1 000 + 72 = 6 000 + 72 = 6 072.

números de dos cifras se multiplican

Ya existe una mano misma se extiende a la calculadora o incluso un lápiz y papel para tomar ventaja de la buena multiplicación de edad en una columna. Aunque no hay nada de enormes proporciones en esta operación allí. Sólo necesita un poco para entrenar la memoria a corto plazo.

Vamos a tratar de multiplicar 47 por 32 dividiendo el proceso en varios pasos.

• 47 × 32 - es la misma que la 47 × (30 + 2) o 47 × 30 + 47 × 2.
• En primer lugar se multiplica 47 por 30. Simplemente la nada: 47 × 3 = 40 × 3 + 7 x 3 = 120 + 21 = 141. Atribuido a la punta del pie derecho y obtener: 1410.
• Off en: 47 = 2 × 40 × 7 × 2 + 2 = 80 + 14 = 94.
• Queda por doblar los resultados: 1 410 + 94 = 1 500 + 4 = 1 504.

Este principio se puede aplicar a los números con un gran número de bits, pero hay que tener en cuenta muchas de las operaciones no son la fuerza de todos.

simplificando la multiplicación

Además de las normas generales, existen varias piratería vida, fácil multiplicación por ciertas cifras de un dígito.

multiplicación en 4

Puede multiplicar el número por 2-valorados, y luego otra vez a las 2.

Ejemplo: 146 × 4 = (146 x 2) x 2 = (200 + 80 + 12) x 2 = 292 × 2 = 400 + 180 + 4 = 584.

multiplicación en 5

Multiplicar el número original de 10 y luego dividir por 2.

Ejemplo: 489 × 5 = 4 890/2 = 2 445.

multiplicación 9

Multiplicar por 10 y luego restar el resultado de la cantidad original.

Ejemplo: 573 × 9 = 5730 - 573 = 5730 - (500 + 70 + 3) = 5 230 - (30 + 40) - 3 = 5 200 - 40 - 3 = 5.16 mil - 3 = 5.157.

multiplicación por 11

La entrada es de la siguiente manera: los primeros y últimos dígitos del número original sustituto delantero y trasero. Una serie se suman todos los números entre ellos.

Cuando se multiplica por un número de dos dígitos, todo se ve muy simple.

Ejemplo: 36 × 11 = 3 (3 + 6) 6 = 396.

Si la cantidad pasa por diez, se mantiene en el centro de las unidades de descarga, y añadir a la primera de un dígito.

Ejemplo: 37 × 11 = 3 (3 + 7) 7 = 3 (10) 7 = 407.

Un poco más complicado con la multiplicación por un número mayor.

Ejemplo: 543 × 11 = 5 (5 + 4) (4 + 3) 3 = 5 973.

¿Cómo aprender a compartir en la mente

Esta es la operación inversa de la multiplicación, por lo que el éxito depende del conocimiento de la totalidad de la misma escuela de la tabla. El resto - una cuestión de práctica.

Dividido por un solo dígito

Para ello, dividimos el número original de varios valores en partes manejables que son exactamente divisible por nuestra inequívoca.

Vamos a tratar de dividir 2.436 por 7.

• 2436 aislar de la parte más grande, que uniformemente dividido en 7. En nuestro caso es 2.100. Obtenemos (2 100 + 336) / 7.
• Seguimos con el mismo espíritu, sólo que ahora con el número 336. Obviamente, 280 dividido por 7. A en el residuo 56 habrá.
• Ahora dividimos cada parte 7: (2 100 + 280 + 56) / 7 = 300 + 40 + 8 = 348.

Dividir por número de dos dígitos

Se trata de las acrobacias aéreas, pero aún tratan.
Supongamos que usted necesita para dividir 1.128 por 24.

• Nos damos cuenta de cuántas veces 24 puede caber en 1128. Obviamente, 1128 es aproximadamente dos veces menos de 24 × 100 (2400). Por lo tanto, por "reducción a cero" tomar multiplicador 50: 24 x 50 = 1.200.
• Hasta 1200 el dividendo 1128 carece de 72. ¿Cuántas veces 24 encajan en 72? Así es, 3. Esto significa que 1.128 = 24 x 50 - 24 × 3 = 24 × (50 - 3) = 24 × 47. En consecuencia, 1128-1124 = 47.

Nosotros no tenemos el ejemplo más difícil, pero utilizando el método de "reducción a cero y la fragmentación en trozos manejables, aprenderá a realizar operaciones más complejas.

Lo que le ayudará a obtener una cuenta orales

Hacer ejercicio todos los días tendrá que llegar a más y más ejemplos, pero si lo hace desearlo. De lo contrario, utilizar otros métodos disponibles.

juegos de mesa

Jugando en aquellos en los que la necesidad de calcular constantemente la mente, usted no sólo aprender a contar rápidamente. Y se combina la utilidad con el pasatiempo agradable con la familia o los amigos.

Tarjetas divertidas como "Uno" y todo tipo de opciones de dominó matemática permite a los estudiantes aprender broma simple suma, resta, multiplicación y división. estrategia económica más complejo al estilo de "Monopoly" para desarrollar talento financiero y habilidades sofisticadas Hone cuenta.

¿Qué comprar

• "Uno";
• "7 9";
• "7 a 9 múltiples»;
• "Atasco";
• "Hekmek";
• "Mathematical Domino";
• "Umnozharium";
• "Código Faraón";
• "Superfermer";
• "Monopoly".

Las aplicaciones móviles

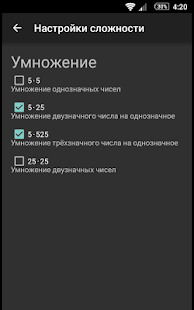
Con ellos se podrá poner el marcador a un automatismo verbal. La mayoría de ellos ofrecen ejemplos de resolver suma, resta, multiplicación y división en el programa de los grados de primaria. Sin embargo, usted se sorprenderá de lo fácil que es. Especialmente si la tarea que tiene que hacer clic en un momento, sin lápiz y papel.

Matemáticas: cálculo mental, la tabla de multiplicar

Cubiertas trabajo de interpretación en el marcador, que corresponden a los grados 1-6 el plan de estudios, incluidas las competencias de los intereses. Se le permite entrenar la velocidad y la calidad de la cuenta, así como ajustar la dificultad. Por ejemplo, desde una simple tabla de multiplicación se puede mover a números de dos y tres dígitos multiplicación y división.

Matemáticas en mente

Otra simple y exposición oral Simulador intuitiva con estadísticas detalladas y dificultad personalizable.

1.001 reto para la cuenta en la mente

La aplicación utiliza los ejemplos de los beneficios de las matemáticas "1001 problema para la cuenta mental", que en el siglo XIX fue un científico y profesor Sergei Raczynski.

trucos de matemáticas

La aplicación le permite aprender fácilmente y discretamente técnicas matemáticas básicas que facilitan y aceleran la cuenta oral. Cada técnica puede funcionar en modo de entrenamiento. Y después de jugar en la velocidad de computación o un oponente.

cerebro rápida

El objetivo - para resolver correctamente como muchos ejemplos matemáticos para un determinado período de tiempo. Los trenes conocimiento de multiplicación, tablas de sumar y restar. Y también contiene un acertijo matemático populares "2048".

Los servicios web

Regularmente ejercicio intelectual con números y puede ser en los simuladores en línea matemáticos. Elegir el tipo de acción deseado y el nivel de dificultad - y hacia adelante, a nuevas alturas intelectuales. Éstas son sólo algunas opciones.

• Matemáticas. club - exposición oral máquina.
• Aristova la escuela - cuenta oral de máquina (que cubre dos dígitos y los números de tres dígitos).
• "Razvivayka" - la formación de la cuenta oral dentro de un centenar.
• 7gy.ru - máquina de matemáticas (cálculo dentro de un centenar).
• Chisloboy - cuenta de juego en línea en el desarrollo de la velocidad.
• niño-mama - formadores de matemáticas para los grados 0-6.